# 平方求幂(快速幂)
是一种简单而有效的小算法,它可以以 的时间复杂度计算乘方
求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积。
在 JS 中,求一个数的幂,方法为 Math.pow (opens new window)
e.g
Maht.pow(2, 3) // => 8
但是,如果我们自己实现一个方法,来计算一个数的幂,相对比较简单,使用 for 循环就可以搞定
function pow(x, n) {
let result = 1
for (let i = 0; i<n; i++) {
result *= x
}
return result
}
假设我们不考虑边界情况,这样的方法就可以使用了,也可以正确的算出结果
pow(2, 3) // => 8
但是当我们算的数值过大时,因为 for 循环的原因,此时就会出现性能问题
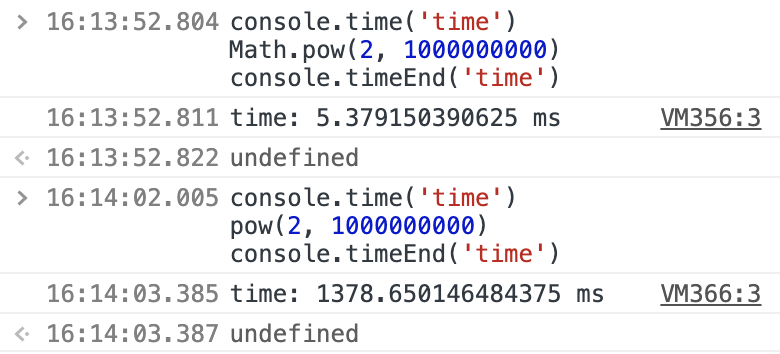
可以看到,同样的算 2 的 10亿次幂,所用的时间是不同的
此时 我们可以看看快速幂是怎么实现的
# 快速幂
举一个简单的例子 求 3 ^ 10 次幂
可以分解为
3 ^ 10 = 3 * 3 * 3 * 3 * 3 * 3 * 3 * 3 * 3 * 3
3 ^ 10 = (3 * 3) * (3 * 3) * (3 * 3) * (3 * 3) * (3 * 3)
3 ^ 10 = (3 * 3) ^ 5
3 ^ 10 = 9 ^ 5
9 ^ 5 = (9 ^ 4) * (9 ^ 1)
9 ^ 5 = (81 ^ 2) * (9 ^ 1)
9 ^ 5 = (6561 ^ 1) * (9 ^ 1)
由此,我们基本是根据 二分法的思路来算 幂,那么我们可以使用 递归来实现上述过程
# 递归快速幂
计算 x 的 n 次方
- 如果 n 是偶数(不为 0),那么就先计算 x 的 n/2 次幂,然后求2次幂;
- 如果 n 是奇数,那么就先计算 x 的 n-1 次幂,再乘上 x;
- 递归结束条件是 x 的 0 次方为 1。
function pow(x, n) {
if (n == 0) return 1;
else if (n % 2 == 1)
return pow(x, n - 1) * x;
else{
let temp = pow(x, n / 2);
return temp * temp;
}
}
如果有些题目要求取结果后三位或者后四位,或者干脆就是让以结果取模
我们可以这么写
function pow(x, n, mod) {
if (n == 0) return 1;
else if (n % 2 == 1)
return pow(x, n - 1) * x % mod;
else{
let temp = pow(x, n / 2) % mod;
return temp * temp % mod;
}
}
这里所用的到取模运算法则,取模的运算法则有很多,
(a + b) % p = (a % p + b % p) % p(a - b) % p = (a % p - b % p ) % p(a * b) % p = (a % p * b % p) % pa ^ b % p = ((a % p)^b) % p- 结合律:
((a+b) % p + c) % p = (a + (b+c) % p) % p ((a*b) % p * c)% p = (a * (b*c) % p) % p- 交换律:
(a + b) % p = (b+a) % p (a * b) % p = (b * a) % p- 分配律:
(a+b) % p = ( a % p + b % p ) % p ((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p
我们主要关注第三条 (a * b) % p = (a % p * b % p) % p,上述代码也就是根据这一条的原理做的改造,也就达到了题目的要求
递归简洁,但是会产生更多的空间,是以空间换时间,我们可以将递归转为循环,避免对栈的浪费,也就是 非递归快速幂
# 非递归快速幂
function pow(x, n) {
let result = 1
while (n) {
if (n % 2) {
result *= x
}
n = Math.floor(n / 2)
x *= x
}
return result
}
使用循环我们也是可以快速计算出结果的,也就是符合了 快速幂的本质 求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积。
对于非递归快速幂,在 JS 中,我们同样可以优化,计算机在计算时,首先会将树转为二进制,然后进行计算,所以我们直接使用 位运算会比较快,同时,可以使用 短路写法去掉 if 判断,改造如下
function pow(x, n) {
let result = 1
while (n) {
(n & 1) && (result *= x)
n >>= 1
x *= x
}
return result
}
这里我们使用 n & 1 代替了 n % 2 的判断,也就是 按位与& (opens new window)
我们以 n 为 奇数和偶数举例,来验证结果的准确性
e.g
a = 1 // 0001
n = 3 // 0011
n & a // 0001 => 1
a = 1 // 0001
n = 4 // 0100
n & a // 0000 => 0
其他奇偶数和上述逻辑相同,由此,我们可以借由 n & 1 来判断 n 的奇偶性
以 n >>= 1 代替了 n = Math.floor(n / 2),有符号右移 (opens new window) 该操作符会将第一个操作数向右移动指定的位数。向右被移出的位被丢弃,拷贝最左侧的位以填充左侧。
e.g
n = 7 // 0111
右移一位,变成
3 // 0011
n = 4 // 0100
// 右移
2 // 0010
右移这里也就相当于, /2 ,向下取整
# e.g
求 2 ^ 1000000000 次幂,最后三位数字
function lastThreeDigits(x, n) {
let result = 1
while (n) {
(n & 1) && (result = result * x % 1000)
n >>= 1
x = x * x % 1000
}
return result
}
console.log(lastThreeDigits(2, 1000000000)) // 376
我们可以看一下运行时间,对比一下
我们以非递归快速幂来做示例,算 2的 10亿次幂
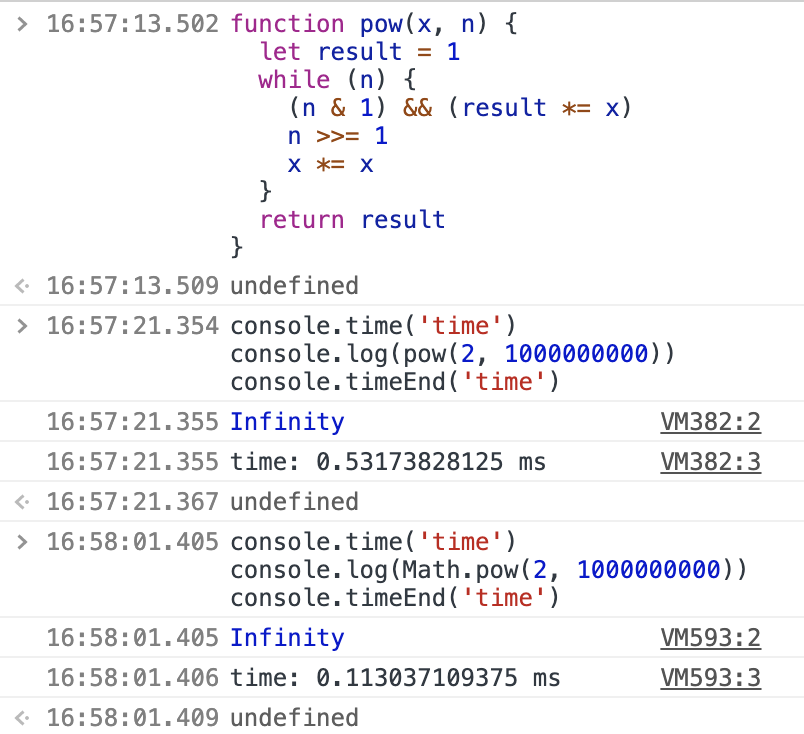
最终的结果超出了最大值,但是时间上相差不大
同样我们可以对比一下一开始的 for 循环写法
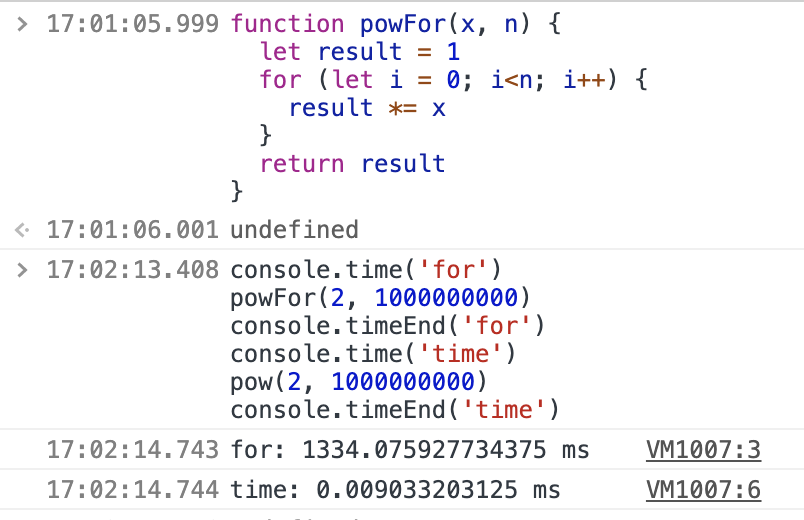
可以看到时间从 1300多 降低到了 零点零几,性能提升一大截
# 最后
快速幂本质也是借鉴了二分法的思想,将循环的过程以2的指数幂做了减少,每次循环都会减半,达到了提升性能的目的。
也就是
求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积。