0.1+0.2 为什么不等于 0.3

不同语言之间的 0.1+0.2 的问题

0.30000000000000004 (opens new window)

在 JavaScript 中

0.1 + 0.2 === 0.3 // false

这是因为 JavaScript 里的数字是采用 IEEE 754 (opens new window) 标准的 64 位双精度浮点数 。该规范定义了浮点数的格式，对于 64 位的浮点数在内存中的表示，最高的 1 位是符号位，接着的 11 位是指数，剩下的 52 位为有效数字，具体：

• 第 0 位：符号位，S 表示 ，0 表示正数，1 表示负数；
• 第 1 位到第 11 位：储存指数部分， Exp 表示 ；
• 第 12 位到第 63 位：储存小数部分（即有效数字），Fraction 表示

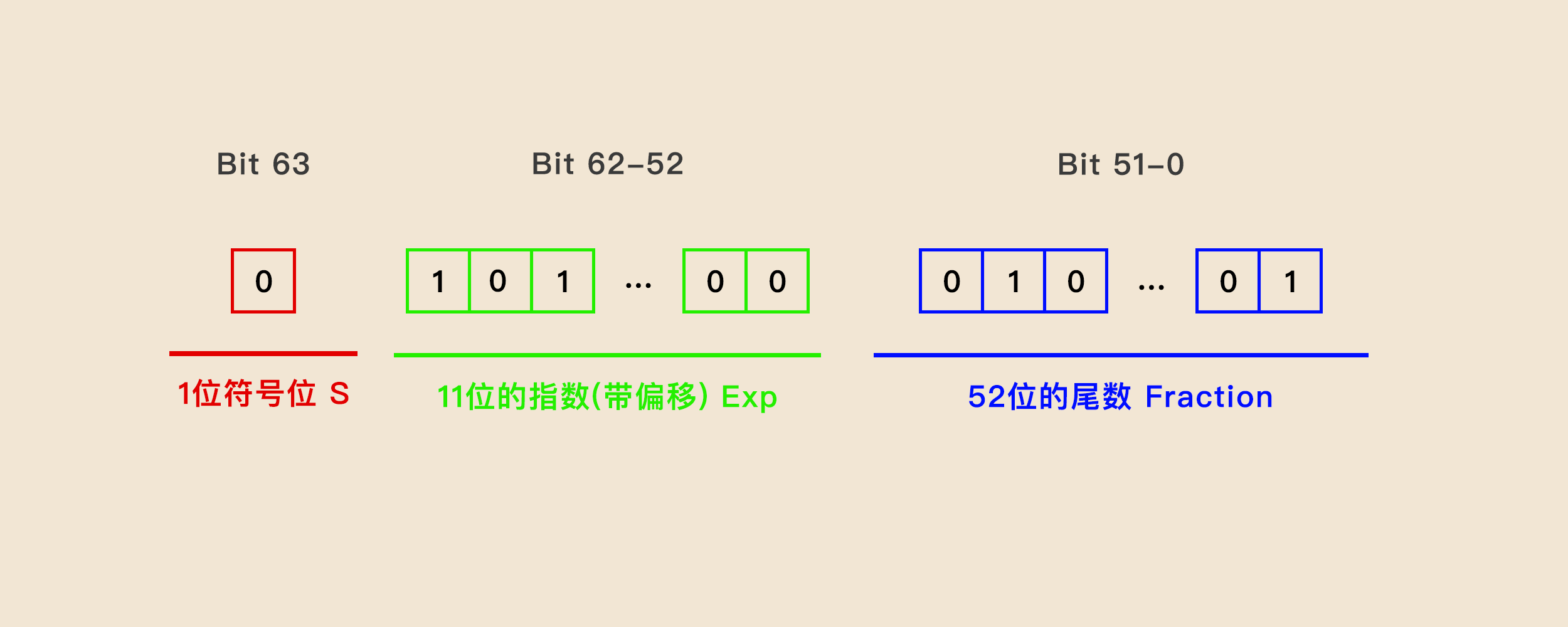
符号位决定正负，指数部分决定数值的大小，小数部分决定数值的精度。

假设有一个数 M

1 < M < 2

也就是说，M 可以写成 1.xxxxxx 的形式，其中 xxxxxx 表示小数部分

IEEE 754 规定，在计算机内部保存 M 时，默认这个数的 第一位总是 1，因此可以被舍去，只保存后面的 xxxxxx 部分。

比如保存 1.01 的时候，只保存 01，等到读取的时候，再把第一位的 1 加上去。这样做的目的，是节省 1 位有效数字。

以 64 位浮点数为例，留给 M 只有 52 位，将第一位的 1 舍去以后，等于可以保存 53 位有效数字。

在 JavaScript 进行计算时，我们用 0.1 + 0.2 来进行举例，在 JavaScript 中，0.1 和 0.2 十进制转为二进制

0.1 => 0.000110011001……(无限)
0.2 => 0.001100110011……(无限)

进制转换的过程如下

// 十进制数 0.1 转二进制计算过程：
0.1*2＝0.2 // ……0—— 整数部分为 “0”。整数部分 “0” 清零后为 “0”，用 “0.2” 接着计算。
0.2*2＝0.4 // ……0—— 整数部分为 “0”。整数部分 “0” 清零后为 “0”，用 “0.4” 接着计算。
0.4*2＝0.8 // ……0—— 整数部分为 “0”。整数部分 “0” 清零后为 “0”，用 “0.8” 接着计算。
0.8*2＝1.6 // ……1—— 整数部分为 “1”。整数部分 “1” 清零后为 “0”，用 “0.6” 接着计算。
0.6*2＝1.2 // ……1—— 整数部分为 “1”。整数部分 “1” 清零后为 “0”，用 “0.2” 接着计算。
0.2*2＝0.4 // ……0—— 整数部分为 “0”。整数部分 “0” 清零后为 “0”，用 “0.4” 接着计算。
0.4*2＝0.8 // ……0—— 整数部分为 “0”。整数部分 “0” 清零后为 “0”，用 “0.8” 接着计算。
0.8*2＝1.6 // ……1—— 整数部分为 “1”。整数部分 “1” 清零后为 “0”，用 “0.6” 接着计算。
0.6*2＝1.2 // ……1—— 整数部分为 “1”。整数部分 “1” 清零后为 “0”，用 “0.2” 接着计算。
0.2*2＝0.4 // ……0—— 整数部分为 “0”。整数部分 “0” 清零后为 “0”，用 “0.4” 接着计算。
0.4*2＝0.8 // ……0—— 整数部分为 “0”。整数部分 “0” 清零后为 “0”，用 “0.2” 接着计算。
0.8*2＝1.6 // ……1—— 整数部分为 “1”。整数部分 “1” 清零后为 “0”，用 “0.2” 接着计算。

所以，得到的整数依次是：0，0，0，1，1，0，0，1，1，0，0，1……

由此，整数部分出现了无限循环。

十进制小数转换成二进制数和十进制整数转换成二进制数不同。十进制整数转换成二进制数需要将得到的余数倒序排列，而十进制小数转换成二进制数只需要将得到的整数按照正常的顺序排列就行了。 最后将十进制原数 0.1 中的整数部分 0 补充到按正常顺序排列的得到的 整数 前面，即：

0.1 (十进制) = 0.0001100110011001 (二进制)

整数的转换是精确的，小数的转换可能出现无穷不循环小数或无限循环小数的情况。此时需要进行舍入处理以截断，所以小数的转换可能略有偏差。

按照 IEEE 754 标准的 64 位双精度浮点数的小数部分最多支持 53 位二进制位，所以两者相加之后得到二进制为

0.0100110011001100110011001100110011001100110011001100

因浮点数小数位的限制而截断的二进制数字，再转换为十进制，就成了 0.30000000000000004 。所以在进行算术计算时会产生误差。